Sistema De Numeração Binário: A Linguagem Dos Computadores – a frase soa complexa, mas a ideia é simples. No coração de cada computador, pulsando em cada processamento, está o sistema binário, uma linguagem de apenas dois dígitos, 0 e 1. Essa aparente simplicidade, porém, sustenta a complexidade de um mundo digital, permitindo que computadores processem informações, de textos e imagens a complexos cálculos científicos.
Vamos desvendar os mistérios dessa linguagem fundamental da era digital.
Este texto explorará os conceitos fundamentais do sistema binário, desde a conversão entre binário e decimal até as operações aritméticas realizadas nesse sistema. Veremos como ele é aplicado na representação de dados em computadores, incluindo texto, imagens e som, e compararemos sua eficiência com outros sistemas de numeração. Prepare-se para mergulhar no fascinante mundo dos bits e bytes!
Conceitos Fundamentais do Sistema Binário
O sistema binário, a base da linguagem dos computadores, difere significativamente do sistema decimal que usamos no dia a dia. Enquanto o sistema decimal utiliza dez dígitos (0 a 9), o sistema binário utiliza apenas dois: 0 e 1. Esta simplicidade é crucial para a construção de circuitos eletrônicos, pois 0 e 1 podem ser facilmente representados por estados elétricos distintos (ausência ou presença de corrente, por exemplo).
A compreensão da estrutura e das operações do sistema binário é fundamental para a programação e a informática em geral.
A conversão entre os sistemas binário e decimal é um processo fundamental. No sistema decimal, cada dígito representa uma potência de 10, começando da direita para a esquerda (unidades, dezenas, centenas, etc.). No sistema binário, cada dígito representa uma potência de
2. Para converter um número binário para decimal, somamos os valores de cada dígito multiplicado pela respectiva potência de
2.
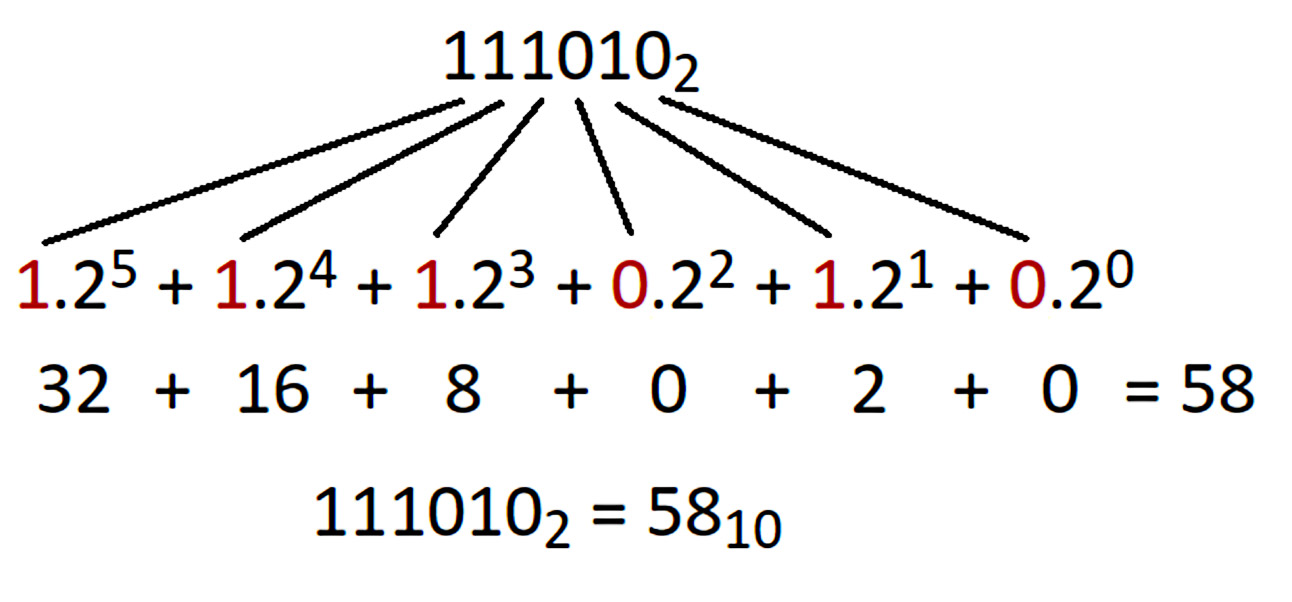
Por exemplo, o número binário 1011 2 é convertido para decimal da seguinte forma: (1 x 2 3) + (0 x 2 2) + (1 x 2 1) + (1 x 2 0) = 8 + 0 + 2 + 1 = 11 10. A conversão de decimal para binário envolve a divisão sucessiva por 2, registrando os restos até o quociente ser 0.
Os restos, lidos de baixo para cima, formam o número binário.
Conversão entre Binário e Decimal
A conversão entre binário e decimal é crucial para a compreensão e manipulação de dados em computadores. A conversão de números inteiros, como demonstrado acima, é relativamente simples. No entanto, a conversão de números fracionários requer um tratamento ligeiramente diferente. Para números fracionários, consideramos potências negativas de 2 à direita da vírgula. Por exemplo, o número binário 101.11 2 é convertido para decimal da seguinte forma: (1 x 2 2) + (0 x 2 1) + (1 x 2 0) + (1 x 2 -1) + (1 x 2 -2) = 4 + 0 + 1 + 0.5 + 0.25 = 5.75 10.
O processo inverso, de decimal para binário fracionário, envolve a multiplicação sucessiva da parte fracionária por 2, registrando a parte inteira do resultado. Este processo continua até que a parte fracionária seja 0 ou se atinja a precisão desejada.
Representação de Números Negativos: Complemento de Dois
Para representar números negativos no sistema binário, utiliza-se comumente o complemento de dois. Este método simplifica a aritmética binária, eliminando a necessidade de circuitos adicionais para lidar com subtrações. O processo para obter o complemento de dois de um número binário é o seguinte: primeiro, encontra-se o complemento de um (invertendo todos os bits, 0s tornam-se 1s e vice-versa); em seguida, soma-se 1 ao resultado.
Por exemplo, para o número decimal -5, representado em 4 bits como 0101 2 (positivo), o complemento de um é 1010 2, e o complemento de dois é 1011 2.
| Decimal | Binário (sem sinal) | Complemento de Dois | Observações |
|---|---|---|---|
| 3 | 0011 | 0011 | Número positivo |
| -3 | 0011 | 1101 | Complemento de dois de 3 |
| 7 | 0111 | 0111 | Número positivo (em 4 bits) |
| -7 | 0111 | 1001 | Complemento de dois de 7 |
Operações Aritméticas em Binário: Sistema De Numeração Binário: A Linguagem Dos Computadores
A aritmética binária, apesar de parecer complexa à primeira vista, é fundamental para o funcionamento dos computadores. Todos os cálculos realizados por um computador, desde os mais simples até os mais complexos, são baseados nas operações aritméticas realizadas em binário. Compreender essas operações é crucial para entender como os computadores processam informações.
Adição Binária, Sistema De Numeração Binário: A Linguagem Dos Computadores
A adição binária segue princípios semelhantes à adição decimal, porém com apenas dois dígitos: 0 e
1. A tabela verdade da adição binária é
0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, e 1 + 1 = 10 (que representa 2 em decimal, pois necessita de um “vai um”). Vejamos alguns exemplos:
1011 + 1101 = 10100
Passo Resultado 1011 + 1101 1 + 1 = 10 (0 e vai 1) 0 1 + 1 + 0 = 10 (0 e vai 1) 00 1 + 0 + 1 = 10 (0 e vai 1) 000 1 + 1 + 1 = 11 1000
110 + 101 = 1011
10110 + 1001 = 11111
111 + 1 = 1000
Algoritmo para Adição Binária:
| Passo | Resultado |
|---|---|
| 1. Inicie da direita para a esquerda, somando os bits correspondentes. | |
| 2. Se a soma for 0 ou 1, anote o resultado. | |
| 3. Se a soma for 2 (1+1), anote 0 e “vai 1” para a próxima coluna. | |
| 4. Repita os passos 2 e 3 para cada coluna. | |
| 5. Se sobrar um “vai 1” ao final, anote-o à esquerda do resultado. |
Subtração Binária

A subtração binária também é semelhante à subtração decimal, utilizando o conceito de “emprestar” quando necessário. Se tentarmos subtrair 1 de 0, precisamos “emprestar” 1 da próxima coluna, que vale 2 em decimal.
1011 – 101 = 100
1101 – 100 = 1001
1000 – 10 = 10
10011 – 101 = 1100
Multiplicação Binária
A multiplicação binária é similar à multiplicação decimal, mas simplificada pela presença de apenas dois dígitos. A multiplicação por 0 resulta em 0, e a multiplicação por 1 resulta no próprio número.
101 x 11 = 1111
110 x 10 = 1100
1001 x 101 = 101101
111 x 11 = 10101
Divisão Binária
A divisão binária segue o mesmo princípio da divisão decimal, utilizando sucessivas subtrações do divisor do dividendo.
1100 / 10 = 110
1011 / 11 = 101
1111 / 101 = 11
10000 / 100 = 100
Em resumo, o sistema de numeração binário é a base da computação moderna, permitindo que máquinas processem e armazenem informações de maneira eficiente. De sua estrutura simples, composta apenas por 0 e 1, surge a capacidade de representar qualquer dado, desde um simples número até complexas imagens em alta resolução. Compreender o funcionamento do sistema binário é essencial para entender como os computadores funcionam e como a tecnologia digital molda nosso mundo.
A jornada pela linguagem dos computadores, portanto, começa com a compreensão desta linguagem fundamental: o binário.

