O Que SãO Retas Paralelas E Segmentos Proporcionais. Cite Exemplos

O Que São Retas Paralelas E Segmentos Proporcionais. Cite Exemplos: No âmbito da geometria, o estudo de retas paralelas e segmentos proporcionais é fundamental para compreender relações espaciais e resolver problemas práticos. Retas paralelas, que nunca se cruzam, e segmentos proporcionais, que mantêm uma razão constante, são conceitos interligados que se aplicam em diversas áreas, desde a arquitetura e engenharia até a cartografia.

Este artigo explora esses conceitos, suas propriedades e aplicações, proporcionando uma visão abrangente de como eles influenciam nosso mundo.

A compreensão de retas paralelas e segmentos proporcionais é crucial para a resolução de problemas de geometria, como calcular distâncias, determinar proporções e analisar formas. Além disso, esses conceitos são amplamente utilizados em áreas como a arquitetura, onde são utilizados para garantir a estabilidade de estruturas, e na engenharia, onde são aplicados no projeto de pontes, edifícios e outras estruturas complexas.

Retas Paralelas

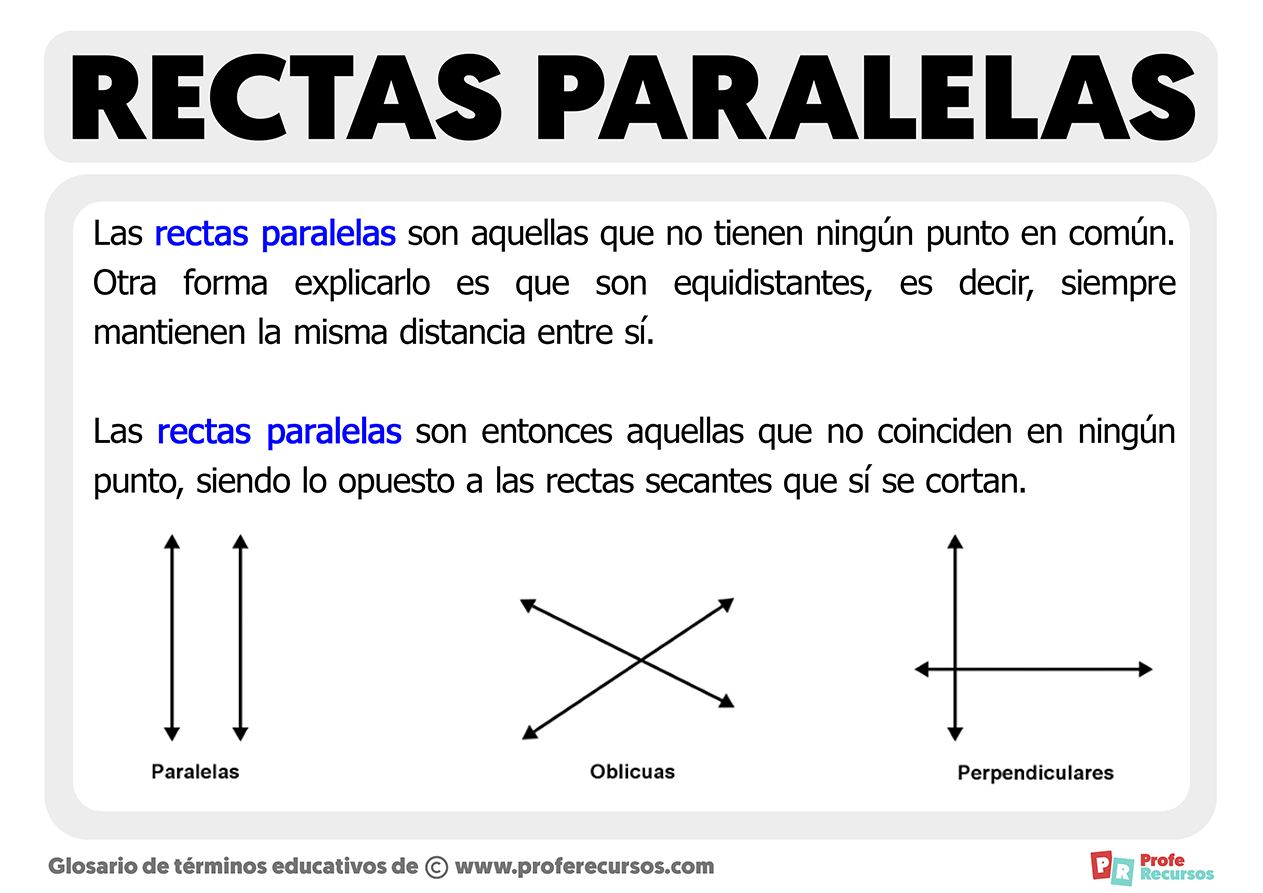
Retas paralelas são um conceito fundamental na geometria, e a sua compreensão é essencial para o estudo de figuras geométricas, como triângulos e quadriláteros.

Duas retas são consideradas paralelas quando estão no mesmo plano e nunca se cruzam, independentemente de quanto sejam prolongadas. A distância entre elas permanece constante em todos os pontos.

Propriedades de Retas Paralelas

As retas paralelas possuem algumas propriedades importantes que as distinguem de outras retas:

• Ângulos Correspondentes:Quando uma reta transversal corta duas retas paralelas, os ângulos correspondentes são iguais. Os ângulos correspondentes são aqueles que ocupam a mesma posição relativa em relação à transversal e às retas paralelas.
• Ângulos Alternos Internos:Os ângulos alternos internos também são iguais. Eles se localizam entre as retas paralelas, em lados opostos da transversal, e ocupam posições inversas.
• Ângulos Colaterais Internos:Os ângulos colaterais internos são suplementares, ou seja, a soma deles é igual a 180 graus. Eles se localizam entre as retas paralelas, do mesmo lado da transversal, e ocupam posições adjacentes.

Exemplos de Retas Paralelas no Mundo Real, O Que São Retas Paralelas E Segmentos Proporcionais. Cite Exemplos:

O conceito de retas paralelas está presente em diversos elementos do nosso cotidiano. Alguns exemplos comuns incluem:

• Trilhos de Trem:Os trilhos de trem são um exemplo clássico de retas paralelas. Eles são projetados para manter os trens em um caminho definido, garantindo que não se desviem da rota.
• Linhas Horizontais em um Prédio:As linhas horizontais em um prédio, como as janelas ou os andares, também são retas paralelas. Elas contribuem para a estética do edifício e ajudam a criar uma sensação de equilíbrio e estabilidade.
• Grades de Rua:As grades de rua, que delimitam as calçadas e as ruas, são compostas por retas paralelas. Elas servem para organizar o espaço urbano e facilitar a circulação de pedestres e veículos.

Segmentos Proporcionais

Segmentos proporcionais são segmentos de reta que mantêm uma relação constante de tamanho entre si. Essa relação é definida por uma razão, que representa a proporção entre os comprimentos dos segmentos. A proporcionalidade entre segmentos é um conceito fundamental na geometria e está diretamente relacionada com o conceito de retas paralelas.

A Relação de Proporção

A razão entre segmentos proporcionais é constante e pode ser expressa como uma fração. Por exemplo, se dois segmentos de reta, AB e CD, são proporcionais, então a razão entre seus comprimentos será sempre a mesma, independentemente do tamanho dos segmentos.

Essa razão é representada por:

AB/CD = k

onde k é uma constante de proporcionalidade.

• Exemplo:Se AB = 6 cm e CD = 3 cm, então a razão entre AB e CD é 6/3 = 2. Isso significa que AB é o dobro do tamanho de CD.

Cálculo da Razão entre Segmentos Proporcionais

Para calcular a razão entre segmentos proporcionais em um diagrama, siga estes passos:

1. Identifique os segmentos proporcionais no diagrama.
2. Meça os comprimentos dos segmentos.
3. Divida o comprimento do primeiro segmento pelo comprimento do segundo segmento.
4. O resultado é a razão entre os segmentos proporcionais.

Exemplos Práticos de Segmentos Proporcionais

Segmentos proporcionais são encontrados em diversas aplicações práticas, como:

• Mapas:Mapas são representações gráficas de áreas geográficas em escala reduzida. As distâncias entre pontos no mapa são proporcionais às distâncias reais no terreno. Por exemplo, se a escala de um mapa é 1:100.000, então 1 cm no mapa corresponde a 100.000 cm (1 km) no terreno.

• Modelos em escala:Modelos em escala, como carros de brinquedo ou maquetes de edifícios, são construídos em uma proporção menor em relação ao objeto real. As dimensões do modelo são proporcionais às dimensões do objeto real.

Teorema de Tales: O Que São Retas Paralelas E Segmentos Proporcionais. Cite Exemplos:

O Teorema de Tales é um princípio fundamental da geometria que estabelece uma relação direta entre retas paralelas e segmentos proporcionais. Ele afirma que, se uma série de retas paralelas intercepta duas retas transversais, os segmentos determinados nas transversais são proporcionais.

Demonstração do Teorema de Tales

O Teorema de Tales pode ser demonstrado utilizando um diagrama que ilustra a relação entre as retas paralelas e os segmentos proporcionais. Considere duas retas transversais, r e s, interceptadas por três retas paralelas, a, b e c.[Diagrama aqui]No diagrama, os segmentos determinados nas transversais r e s são:* Em r:AB, BC, CD

Em s

A’B’, B’C’, C’D’O Teorema de Tales afirma que:

AB/A’B’ = BC/B’C’ = CD/C’D’

Em outras palavras, a razão entre os segmentos correspondentes nas duas transversais é constante.

Aplicações do Teorema de Tales

O Teorema de Tales possui diversas aplicações na resolução de problemas de geometria, incluindo:* Cálculo de comprimentos de segmentos:O teorema pode ser utilizado para calcular o comprimento de um segmento desconhecido em uma figura, se os comprimentos dos outros segmentos e a proporção entre eles forem conhecidos.

Determinação de paralelismo

Se a razão entre os segmentos determinados por três retas em uma transversal é constante, então as três retas são paralelas.

Divisão de segmentos em partes proporcionais

O teorema pode ser usado para dividir um segmento em partes proporcionais a outros segmentos. Exemplo:Considere um triângulo ABC, onde DE é paralelo a BC. Se AB = 10 cm, AD = 4 cm e AC = 15 cm, determine o comprimento de AE.[Diagrama aqui]Aplicando o Teorema de Tales:

AD/AB = AE/AC

Substituindo os valores conhecidos:

4/10 = AE/15

Resolvendo para AE:

AE = (4/10)

15 = 6 cm

Portanto, o comprimento de AE é 6 cm.

Question & Answer Hub

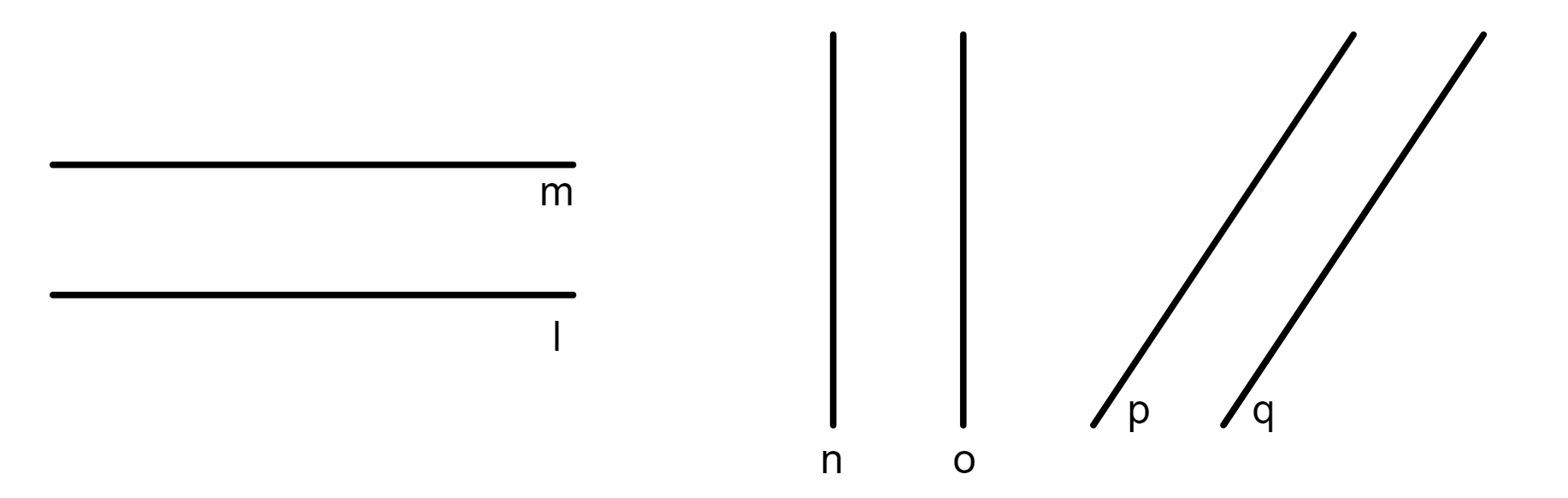
Como posso identificar retas paralelas em um diagrama?

Retas paralelas nunca se cruzam, mesmo quando estendidas infinitamente. Em um diagrama, elas geralmente são indicadas por setas paralelas ou por um símbolo de paralelismo (//).

Quais são as propriedades de segmentos proporcionais?

Segmentos proporcionais mantêm uma razão constante. Se dois segmentos são proporcionais, a razão entre suas medidas é a mesma, independentemente do tamanho dos segmentos.

O Teorema de Tales pode ser aplicado em qualquer triângulo?

O Teorema de Tales é aplicado em triângulos onde duas retas paralelas intersectam os lados do triângulo, criando segmentos proporcionais.