Distribuição Normal Exemplos A Media De 50 Acima De 50 – A Distribuição Normal: Exemplos com Média 50 e Valores Acima é um conceito fundamental na estatística, que descreve a distribuição de dados em torno de um valor central. Essa distribuição, também conhecida como curva em forma de sino, é frequentemente encontrada em fenômenos naturais e sociais, como a altura de pessoas, a pressão arterial ou os resultados de testes padronizados.
Neste estudo, exploraremos como a média de 50 afeta a forma da curva da Distribuição Normal e a probabilidade de encontrar valores acima desse ponto. Investigaremos o impacto do desvio padrão na dispersão dos dados e como a Distribuição Normal é aplicada em diversas áreas, desde a medicina até a engenharia.
Introdução à Distribuição Normal
A Distribuição Normal, também conhecida como Curva de Gauss ou Curva em Forma de Sino, é uma das distribuições de probabilidade mais importantes e amplamente utilizadas em estatística. Ela descreve a distribuição de dados que tendem a se agrupar em torno de um valor central, com valores mais baixos e mais altos ocorrendo com menor frequência.
Essa distribuição é caracterizada por sua forma simétrica e em forma de sino, com a maior parte dos dados concentrados na média.
Características da Distribuição Normal
- Simetria:A curva é simétrica em relação à média, o que significa que a metade dos dados está abaixo da média e a outra metade está acima.
- Forma de Sino:A curva tem a forma de um sino, com um pico na média e declives suaves em direção às extremidades.
- Média, Mediana e Moda Coincidem:Na Distribuição Normal, a média, a mediana e a moda são todas iguais.
- Desvio Padrão:O desvio padrão mede a dispersão dos dados em torno da média. Um desvio padrão maior indica uma maior dispersão, enquanto um desvio padrão menor indica uma menor dispersão.
O Conceito de Média na Distribuição Normal
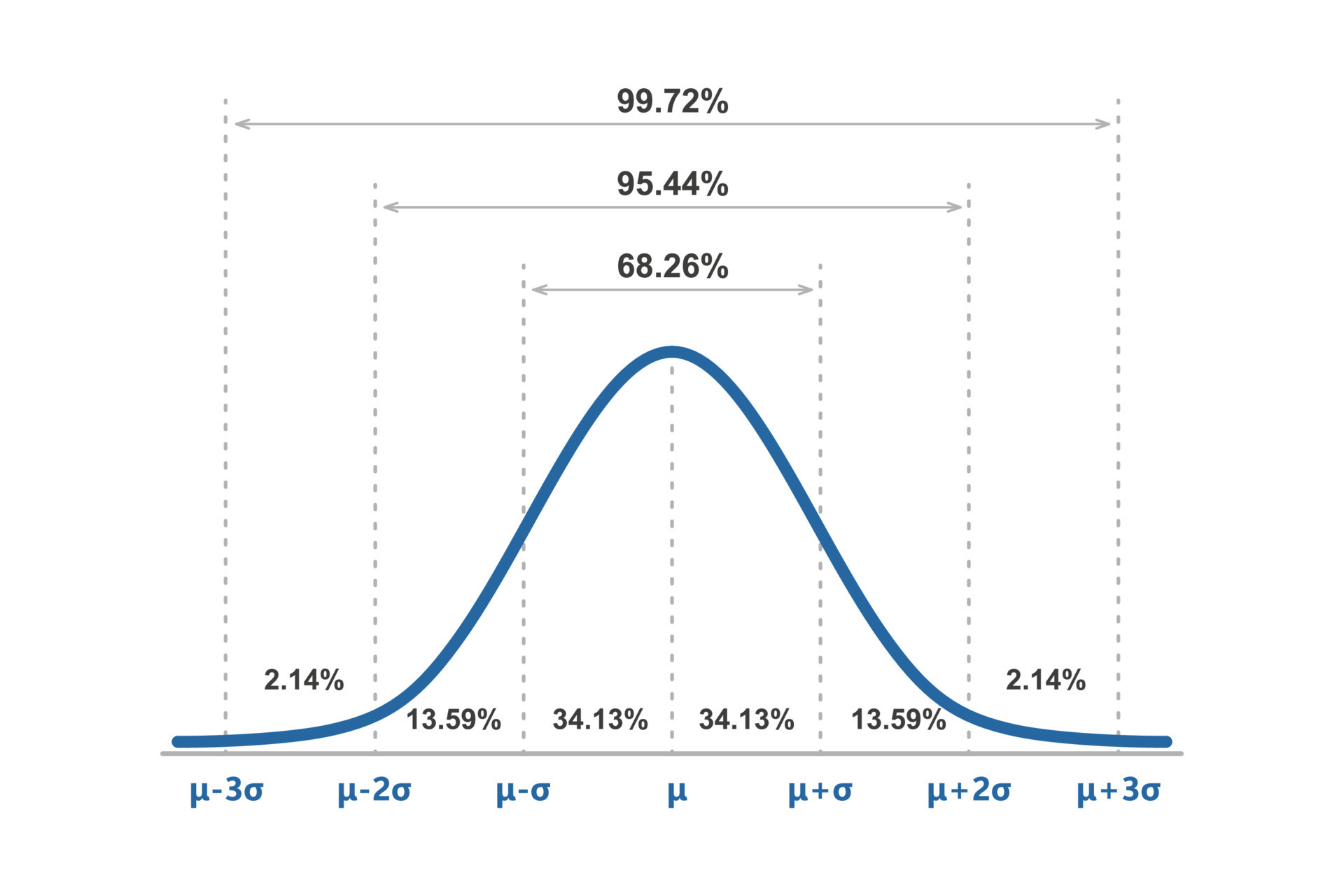
A média é o valor central da Distribuição Normal e representa o ponto onde a maioria dos dados se concentra. Ela é um importante parâmetro que define a localização da curva na linha numérica. A média é frequentemente representada pela letra grega μ (mi).
Exemplos de Fenômenos que Seguem a Distribuição Normal
- Altura de Pessoas:A altura de uma população geralmente se distribui normalmente, com a maioria das pessoas tendo uma altura próxima à média.
- Pressão Arterial:A pressão arterial de uma população também tende a seguir uma distribuição normal, com a maioria das pessoas tendo uma pressão arterial próxima à média.
- Resultados de Testes:Os resultados de testes padronizados, como o SAT ou o ENEM, geralmente se distribuem normalmente.
A Distribuição Normal com Média 50
Uma Distribuição Normal com média 50 é uma distribuição de probabilidade onde o valor central ou a média é igual a 50. Isso significa que a maior parte dos dados se concentra em torno do valor 50, com valores mais baixos e mais altos ocorrendo com menor frequência.
A Média de 50 Afeta a Forma da Curva
A média de 50 define a localização da curva na linha numérica. A curva será centrada no valor 50, e a forma da curva permanecerá a mesma, com a mesma simetria e forma de sino. O que muda é a localização do pico da curva, que estará no valor 50.
Gráfico da Distribuição Normal com Média 50
O gráfico da Distribuição Normal com média 50 pode ser apresentado com diferentes valores de desvio padrão. Por exemplo, um desvio padrão de 10 resultaria em uma curva mais dispersa, enquanto um desvio padrão de 5 resultaria em uma curva mais concentrada.
Imagine um gráfico com a forma de sino. O eixo horizontal representa os valores da variável (por exemplo, altura, pressão arterial) e o eixo vertical representa a frequência ou probabilidade de cada valor. O pico da curva está localizado no valor 50, e a forma da curva depende do desvio padrão.
Valores Acima de 50
Em uma Distribuição Normal com média 50, a probabilidade de encontrar valores acima de 50 depende do desvio padrão. Um desvio padrão maior significa uma maior dispersão dos dados, resultando em uma maior probabilidade de encontrar valores acima de 50.
Por outro lado, um desvio padrão menor significa uma menor dispersão dos dados, resultando em uma menor probabilidade de encontrar valores acima de 50.
Influência do Desvio Padrão
O desvio padrão determina a largura da curva da Distribuição Normal. Quanto maior o desvio padrão, mais ampla a curva e maior a probabilidade de encontrar valores mais distantes da média.
Probabilidades de Valores Acima de 50
| Desvio Padrão | Probabilidade de Valores Acima de 50 |
|---|---|
| 5 | 34.13% |
| 10 | 15.87% |
| 15 | 4.96% |
Aplicações da Distribuição Normal: Distribuição Normal Exemplos A Media De 50 Acima De 50
A Distribuição Normal é uma ferramenta poderosa com aplicações em diversas áreas, incluindo estatística, medicina e engenharia.
Aplicações em Estatística
- Análise de Dados:A Distribuição Normal é utilizada para analisar dados e determinar se eles se distribuem normalmente. Isso permite aos estatísticos fazer inferências sobre a população a partir de uma amostra.
- Teste de Hipóteses:A Distribuição Normal é usada em testes de hipóteses para determinar se há evidências suficientes para rejeitar uma hipótese nula.
- Construção de Intervalos de Confiança:A Distribuição Normal é usada para construir intervalos de confiança para estimar a média de uma população.
Aplicações em Medicina
- Controle de Qualidade:A Distribuição Normal é utilizada para controlar a qualidade de produtos farmacêuticos e dispositivos médicos, garantindo que eles atendam aos padrões de segurança e eficácia.
- Pesquisa Clínica:A Distribuição Normal é usada em pesquisas clínicas para analisar dados de pacientes e determinar a eficácia de tratamentos.
- Diagnóstico Médico:A Distribuição Normal pode ser utilizada para ajudar a diagnosticar doenças, comparando os valores de um paciente com os valores normais da população.
Aplicações em Engenharia
- Controle de Qualidade:A Distribuição Normal é utilizada para controlar a qualidade de produtos manufaturados, garantindo que eles atendam aos padrões de desempenho.
- Análise de Riscos:A Distribuição Normal é usada para analisar riscos em projetos de engenharia, como a probabilidade de falhas em estruturas.
- Simulação:A Distribuição Normal é usada em simulações de engenharia para modelar fenômenos aleatórios, como o vento ou as ondas.
Considerações Adicionais
Apesar de sua ampla aplicabilidade, a Distribuição Normal tem suas limitações. É importante entender esses limites e as diferenças entre a Distribuição Normal e outras distribuições de probabilidade.
Limites da Distribuição Normal
- Dados Assimétricos:A Distribuição Normal não é adequada para modelar dados que são assimétricos, ou seja, dados que não se distribuem igualmente em torno da média.
- Valores Extremos:A Distribuição Normal não é adequada para modelar dados que contêm valores extremos, ou seja, valores que são muito altos ou muito baixos em relação à média.
- Dados Discretos:A Distribuição Normal é uma distribuição contínua, o que significa que ela não é adequada para modelar dados discretos, ou seja, dados que podem assumir apenas valores específicos.
Diferenças Entre a Distribuição Normal e Outras Distribuições
Existem outras distribuições de probabilidade que podem ser mais adequadas para modelar dados que não se distribuem normalmente. Algumas das distribuições mais comuns incluem:
- Distribuição Binomial:Adequada para modelar o número de sucessos em uma série de ensaios independentes.
- Distribuição de Poisson:Adequada para modelar o número de eventos que ocorrem em um determinado período de tempo ou lugar.
- Distribuição Exponencial:Adequada para modelar o tempo até que um evento ocorra.
Desafios e Oportunidades
A aplicação da Distribuição Normal em diferentes áreas apresenta desafios e oportunidades. É essencial escolher a distribuição correta para modelar os dados, levando em consideração as características dos dados e o objetivo da análise. A Distribuição Normal é uma ferramenta poderosa, mas é importante entender seus limites e as alternativas disponíveis para garantir análises precisas e confiáveis.

